Acwing刷题记录

Cpp
算法
发布日期:   2021-03-23
更新日期:   2023-09-11
文章字数:   11.6k
阅读时长:   64 分
阅读次数:  

前言

本文记录本人刷Acwing过程的收获和代码。语言选择C++。

1～1000

1～500

1～100

2.01背包问题

因为这道题只使用了f[i-1]且j-v[i]<=j，因此可以使用滚动数组优化。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <iostream>

using namespace std;
const int N = 1001;
int v[N], w[N];
int f[N][N];
int ff[N];

void twoDimension(int n, int m) {
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= m; ++j) {
            f[i][j] = f[i - 1][j];
            if (j >= v[i]) {
                f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
            }
        }
    }
    printf("%d\n", f[n][m]);
}

void oneDimension(int n, int m) {
    for (int i = 1; i <= n; ++i) {
        for (int j = m; j >= v[i]; --j) {
            ff[j] = max(ff[j], ff[j - v[i]] + w[i]);
        }
    }
    printf("%d\n", ff[m]);
}

int main() {
    int n, m;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; ++i) scanf("%d%d", &v[i], &w[i]);
    oneDimension(n, m);
    return 0;
}
19. 二叉树的下一个节点

这题主要想法就是判断当前节点是否拥有右节点。如果拥有右节点，则中序遍历的后一个节点为右节点子树的最左的节点。即，通过右节点循环找到子树的最左的节点；如果没有右节点，则中序遍历的后一个节点为该节点父节点的拐点。即上一次子树的根节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    TreeNode* inorderSuccessor(TreeNode* p) {
        if(!p) return nullptr;
        //有右节点的情况
        if(p->right){
            p=p->right;
            while(p->left)
                p=p->left;
            return p;
        }else{
            //没有右节点的情况
            while(p->father&&p->father->right==p) p=p->father;
            return p->father;
        }
    }
};
26. 二进制中1的个数
1
2
3
4
5
6
7
8
class Solution {
public:
    int NumberOf1(int n) {
        int res=0;
        while(n) n-=n&-n,res+=1;
        return res;
    }
};
33. 链表中倒数第k个节点

本题解题分为两步：

  1. 计算当前链表长度
  2. 通过n-k循环找到返回的节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    ListNode* findKthToTail(ListNode* pListHead, int k) {
        if(!pListHead) return NULL;
        int len=0;
        for(auto p=pListHead;p;p=p->next) len+=1;
        if(k>len)return NULL;
        else{
            auto p=pListHead;
            for(int i=0;i<len-k;i++) p=p->next;
            return p;
        }
    }
};
35. 反转链表

此题有两个版本，一个迭代，一个递归。

迭代版：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        //如果没有节点或者只有一个节点
        if(head==NULL||head->next==NULL) return head;
        auto current=head;
        ListNode* pre=NULL;
        while(current){
            auto next=current->next;
            current->next=pre;
            //为下一l
            pre=current;
            current=next;
        }
        return pre;
    }
};

递归版：

1

77.翻转单词顺序

本题分为二步：

  1. 首先将整个字符串进行翻转
  2. 将每个字母进行翻转。此处用双指针算法，设置j获取当前字母长度，进行翻转
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    string reverseWords(string s) {
        reverse(s.begin(),s.end());
        for(int i=0;i<s.size();i++){
            int j=i+1;
            while(s[j]!=' '&&j<s.size()) j++;
            reverse(s.begin()+i,s.begin()+j);
            i=j;
        }
        return s;
    }
};

101~200

154.滑动窗口

本题利用了结果本身的单调性。因为滑动窗口的长度限制，所以使用单调队列而非单调栈。当新元素入队的时候，元素从队尾移除。当新入队元素小于(或大于)等于队尾元素时，将相应元素从队尾出队。生成的单调队列具有单调性，其最值即为队尾或队首元素。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <iostream>
using namespace std;
const int N = 1e6 + 10;
//q数组负责记录提供的数据，s数组负责记录q数组对应元素的索引
int q[N], s[N];
//hh表示单调队列的头部，tt表示单调队列的尾部
int hh = 0, tt = -1;

int main() {
    int n, k;
    scanf("%d%d", &n, &k);
    for (int i = 0; i < n; ++i) scanf("%d", &q[i]);
    for (int i = 0; i < n; ++i) {
        //检查队头是否出队列
        if (hh <= tt && i - k + 1 > s[hh]) ++hh;
        //检查单调队列队尾元素是否大于等于新入队元素
        while (hh <= tt && q[s[tt]] >= q[i]) --tt;
        //新元素入队
        s[++tt] = i;
        if (i >= k - 1) printf("%d ", q[s[hh]]);
    }
    printf("\n");
    //重新初始化
    hh = 0, tt = -1;
    for (int i = 0; i < n; ++i) {
        //检查队头是否出队列
        if (hh <= tt && i - k + 1 > s[hh]) ++hh;
        //检查单调队列队尾元素是否小于等于新入队元素
        while (hh <= tt && q[s[tt]] <= q[i]) --tt;
        //新元素入队
        s[++tt] = i;
        if (i >= k - 1) printf("%d ", q[s[hh]]);
    }
    return 0;
}
197. 阶乘分解

质数定理：不超过x的质数的个数近似为。

底数为10时，对数可简写为。

底数为e时，对数可简写为。

201~300

257.关押罪犯
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include <cstdio>
#include <cstring>

const int N = 2e4 + 10, M = 2e5 + 10;
int n, m;
int e[M], ne[M], idx, h[N], w[M];
int color[N];

void add(int x, int y, int c) {
    e[idx] = y;
    w[idx] = c;
    ne[idx] = h[x];
    h[x] = idx++;
}

bool dfs(int index, int c, int mid) {
    color[index] = c;
    for (int i = h[index]; ~i; i = ne[i]) {
        int j = e[i];
        if (w[i] <= mid) continue;
        if (color[j] == -1) {
            if (!dfs(j, !c, mid)) return false;
        } else if (color[j] == c) return false;
    }
    return true;
}

bool check(int mid) {
    memset(color, -1, sizeof color);
    for (int i = 1; i <= n; ++i) {
        if (!~color[i]) {
            if (!dfs(i, 0, mid)) return false;
        }
    }
    return true;
}

int main() {
    scanf("%d%d", &n, &m);
    memset(h,-1,sizeof h);
    int x, y, w;
    for (int i = 0; i < m; ++i) {
        scanf("%d%d%d", &x, &y, &w);
        add(x, y, w), add(y, x, w);
    }
    int l = 0, r = 1e9, mid;
    while (l < r) {
        mid = l + r >> 1;
        if (check(mid))r = mid;
        else l = mid + 1;
    }
    printf("%d", l);
    return 0;
}

301~400

401~500

501～1000

501~600

601~700

643. 动态网格

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <cstring>
#include <iostream>

using namespace std;
char nums[101][101];
int r, c;
bool st[101][101];
const int dx[4] = {1, -1, 0, 0}, dy[4] = {0, 0, 1, -1};

void dfs(int x, int y) {
    st[x][y] = true;
    for (int i = 0; i < 4; ++i) {
        int tx = x + dx[i], ty = y + dy[i];
        if (tx >= 0 && tx < r && ty >= 0 && ty < c && st[tx][ty] == false && nums[tx][ty] == '1') dfs(tx, ty);
    }
}

int query() {
    memset(st, 0, sizeof st);
    int res = 0;
    for (int i = 0; i < r; ++i) {
        for (int j = 0; j < c; ++j) {
            if (!st[i][j] && nums[i][j] == '1') {
                res += 1;
                dfs(i, j);
            }
        }
    }
    return res;
}

int main() {
    int t;
    cin >> t;
    for (int i = 1; i <= t; ++i) {
        cout << "Case #" << i << ":" << endl;
        cin >> r >> c;
        for (int j = 0; j < r; ++j) cin >> nums[j];
        int n;
        cin >> n;
        char op;
        while (n--) {
            cin >> op;
            if (op == 'M') {
                int x, y, z;
                cin >> x >> y >> z;
                nums[x][y] = '0' + z;
            }
            if (op == 'Q') cout << query() << endl;
        }
    }
    return 0;
}

701~800

785. 快速排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include <iostream>

using namespace std;
const int N = 1e6 + 10;
int q[N];

void quicksort(int q[], int l, int r) {
    if (l >= r) return;
    int x = q[l + r >> 1];
    int i = l - 1, j = r + 1;
    while (i < j) {
        do i++; while (q[i] < x);
        do j--; while (q[j] > x);
        if (i<j) swap(q[i],q[j]);
    }
    quicksort(q,l,j);
    quicksort(q,j+1,r);
}

int main() {
    int n;
    scanf("%d", &n);
    for (int i = 0; i < n; i++) scanf("%d", &q[i]);
    quicksort(q, 0, n - 1);
    for (int i = 0; i < n; i++) printf("%d ", q[i]);
    return 0;
}
786.第k个数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/**
 * 本题的解题思路：
 * 直接使用快排的时间复杂度是O(nlogn)
 * 这题可以结合二分与快排的思想，将时间复杂度优化到O(n)
 * 重点在于进行一次快排后，如果第k个数在快排的小于x的部分时，相应的缩小快排空间。同理，另一个区间也是一样
 */
#include <iostream>

using namespace std;
const int N = 1e6 + 10;
int q[N];

int quick_select(int l, int r, int k) {
    //如果当前区间只有一个元素，则其必然是答案
    if (l == r) return q[l];
    int x = q[(l + r) / 2], i = l - 1, j = r + 1;
    while (i < j) {
        while (q[++i] < x);
        while (q[--j] > x);
        if (i < j) swap(q[i], q[j]);
    }
    int sl = j - l + 1;
    if (k <= sl) return quick_select(l, j, k);
    return quick_select(j + 1, r, k - sl);
}

int main() {
    int n, k;
    scanf("%d %d", &n, &k);
    for (int i = 0; i < n; i++) scanf("%d", &q[i]);
    printf("%d\n", quick_select(0, n - 1, k));
    return 0;
}
787. 归并排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include <iostream>

using namespace std;
const int N = 1e6 + 10;
int q[N], tmp[N];

void merge_sort(int q[], int l, int r) {
    if (l >= r) return;
    int mid = (l + r) >> 1;
    merge_sort(q,l, mid), merge_sort(q,mid + 1, r);
    int i = l, j = mid + 1, k = 0;
    while (i <= mid && j <= r) {
        if (q[i] <= q[j]) tmp[k++] = q[i++];
        else tmp[k++] = q[j++];
    }
    while (i <= mid) tmp[k++] = q[i++];
    while (j <= r) tmp[k++] = q[j++];
    for(i=l,j=0;i<=r;i++,j++) q[i]= tmp[j];
}

int main() {
    int n;
    scanf("%d", &n);
    for (int i = 0; i < n; i++) scanf("%d ", &q[i]);
    merge_sort(q, 0, n - 1);
    for (int i = 0; i < n; i++) printf("%d", q[i]);
    return 0;
}
788.逆序对的数量

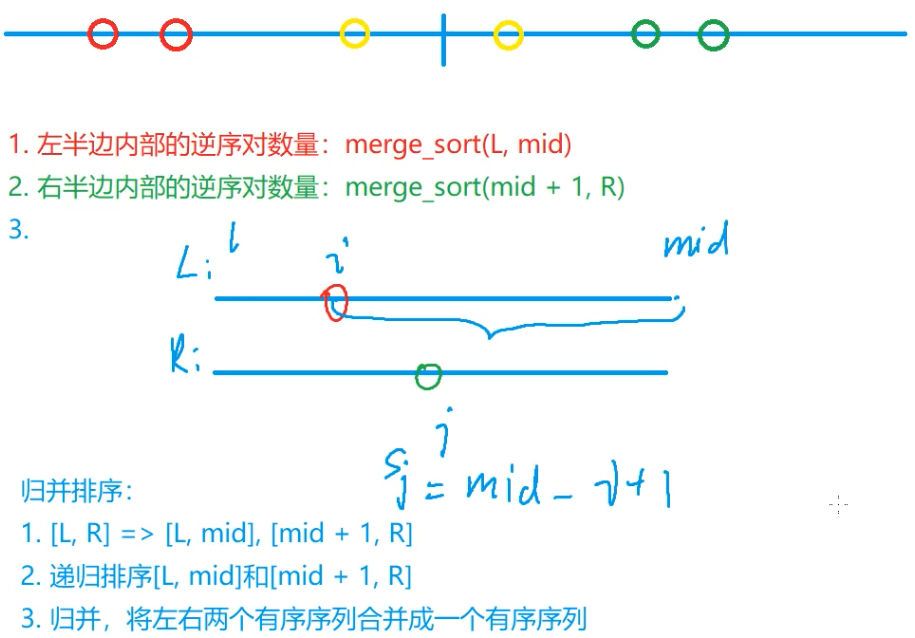
788逆序对的数量.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
```



##### [789. 数的范围](https://www.acwing.com/problem/content/791/)

```cpp
#include < iostream >

const int N = 10010;

int n, m;
int q[N];

int main() {
    scanf("%d %d", &n, &m);
    for (int i = 0; i < n; ++i) {
        scanf("%d", &q[i]);
    }
    while (m--) {
        int x;
        scanf("%d", &x);
        int l = 0, r = n - 1;
        while (l < r) {
            int mid = l + r >> 1;
            if (q[mid] >= x) {
                r = mid;
            } else {
                l = mid + 1;
            }
        }
        if (q[l] != x) {
            std::cout << "-1 -1" << std::endl;
        } else {
            std::cout << l << " ";
            int l = 0, r = n - 1;
            while (l < r) {
                int mid = l + r + 1 >> 1;
                if (q[mid] <= x) {
                    l = mid;
                } else {
                    r = mid - 1;
                }
            }
            std::cout << l << std::endl;
        }
    }
    return 0;
}
790. 数的三次方根

本题需要主要三次方的时候，当数字是0.001之类的小于1的数时，寻找范围需要扩大。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include <iostream>

using namespace std;

int main() {
    double x;
    scanf("%lf", &x);
    if (x < 0) {
        printf("-");
        x = -x;
    }
    double l = 0, r = x, mid;
    if (x<1) r=1;
    while (r - l >= 1e-8) {
        mid = (r + l) / 2;
        if (mid * mid * mid > x) r = mid;
        else l = mid;
    }
    printf("%lf", mid);
    return 0;
}
791. 高精度加法

这里的选择使用数组存储大整数，这里第0位存个位数，最高位放在数组最后面。这样当发生进位的时候，容易处理。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include <iostream>
#include <vector>

using namespace std;
const int N = 16 + 10;

vector<int> add(vector<int> &A, vector<int> &B) {
    vector<int> C;
    int t = 0;
    for (int i = 0; i < A.size() || i < B.size(); i++) {
        if (i < A.size()) t += A[i];
        if (i < B.size()) t += B[i];
        C.push_back(t % 10);
        t /= 10;
    }
    if (t) C.push_back(t);
    return C;
}

int main() {
    vector<int> A, B;
    string a, b;
    cin >> a >> b;
    for (int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0');
    for (int i = b.size() - 1; i >= 0; --i) B.push_back(b[i] - '0');
    auto c = add(A, B);
    for (int i = c.size() - 1; i >= 0; --i) printf("%d", c[i]);
    return 0;
}
792. 高精度减法

记得去掉结果中多余的0.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include <iostream>
#include <vector>

using namespace std;

vector<int> sub(vector<int> &A, vector<int> &B) {
    vector<int> C;
    int t = 0;
    for (int i = 0; i < A.size(); i++) {
        t = A[i] - t;
        if (i < B.size()) t -= B[i];
        C.push_back((t + 10) % 10);
        if (t < 0) t = 1;
        else t = 0;
    }
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

//A>=B
bool cmp(vector<int> &A, vector<int> &B) {
    if (A.size() != B.size()) return A.size() > B.size();
    else {
        for (int i = A.size() - 1; i >= 0; --i) {
            if (A[i] != B[i]) return A[i] > B[i];
        }
    }
    return true;
}

int main() {
    string a, b;
    cin >> a >> b;
    vector<int> A, B;
    for (int i = a.size() - 1; i >= 0; i--) A.push_back(a[i]-'0');
    for (int i = b.size() - 1; i >= 0; i--) B.push_back(b[i]-'0');
    if (cmp(A, B)) {
        auto C = sub(A, B);
        for (int i = C.size() - 1; i >= 0; i--) printf("%d", C[i]);
    } else {
        auto C = sub(B, A);
        printf("-");
        for (int i = C.size() - 1; i >= 0; i--) printf("%d", C[i]);
    }
    return 0;
}
793. 高精度乘法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include <iostream>
#include <vector>

using namespace std;

vector<int> mul(vector<int> &A, int B) {
    vector<int> C;
    int t = 0;
    for (int i = 0; i < A.size() || t; i++) {
        if (i < A.size()) t += A[i] * B;
        C.push_back(t % 10);
        t /= 10;
    }
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

int main() {
    string a;
    vector<int> A;
    int b;
    cin >> a >> b;
    for (int i = a.size() - 1; i >= 0; --i) A.push_back(a[i] - '0');
    auto C = mul(A, b);
    for (int i = C.size() - 1; i >= 0; i--) printf("%d", C[i]);
    return 0;
}
794. 高精度除法

除法这里需要注意，运算从高位开始处理。所以需要反过来进行处理。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

vector<int> div(vector<int> &A, int b, int &r) {
    vector<int> C;
    for (int i = A.size() - 1; i >= 0; i--) {
        r = r * 10 + A[i];
        C.push_back(r / b);
        r %= b;
    }
    reverse(C.begin(), C.end());
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

int main() {
    string a;
    int b;
    vector<int> A;
    cin >> a >> b;
    for (int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0');
    //r为余数
    int r = 0;
    auto C = div(A, b, r);
    for (int i = C.size() - 1; i >= 0; i--) printf("%d", C[i]);
    printf("\n%d", r);
    return 0;
}
795. 前缀和

本题使用的是一维前缀和。注意这里的s数组存放前缀和，相减的时候需要将左边界-1。s[0],a[0]处放0，以便后续操作。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <iostream>

using namespace std;
const int N = 1e6 + 10;
int q[N];
int s[N];

int main() {
    int n, m;
    s[0] = 0;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; ++i) {
        scanf("%d", &q[i]);
        s[i] = s[i - 1] + q[i];
    }
    while (m--) {
        int l, r;
        scanf("%d%d", &l, &r);
        printf("%d\n", s[r] - s[l - 1]);
    }
    return 0;
}
796. 子矩阵的和

本题依旧是前缀和，不过是二维前缀和，重点就两个公式。此处假设S为前缀和数组，q为相应的差分数组。

更新前缀和数组：

计算前缀和之差：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <iostream>

using namespace std;
const int N = 1010;
int x[N][N], s[N][N];

int main() {
    int n, m, q;
    scanf("%d%d%d", &n, &m, &q);
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= m; ++j) {
            scanf("%d", &x[i][j]);
            s[i][j] = s[i][j - 1] + s[i - 1][j] - s[i - 1][j - 1] + x[i][j];
        }
    }
    int x1, y1, x2, y2;
    while (q--) {
        scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
        printf("%d\n", s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]);
    }
    return 0;
}
797. 差分
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <iostream>

using namespace std;
const int N = 1e6 + 10;
// q数组为原数组,b数组为差分数组
int q[N], b[N];
void insert(int l,int r,int c){
    b[l]+=c;
    b[r+1]-=c;
}

int main() {
    int n, m;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++) {
        scanf("%d", &q[i]);
        //step1 构造差分数组
        insert(i,i,q[i]);
    }
    //step2 更新差分数组信息
    int l,r,c;
    while (m--) {
        scanf("%d%d%d",&l,&r,&c);
        insert(l,r,c);
    }
    //step3 更新前缀和,需要注意这里是在差分数组的基础上进行前缀和的计算，所以都是+=操作
    //此处的b数组成为前缀和数组
    for(int i=1;i<=n;i++) {
        b[i]+=b[i-1];
        printf("%d ",b[i]);
    }
    return 0;
}
798. 差分矩阵
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <iostream>

using namespace std;
const int N = 1010;
int a[N][N], s[N][N];

//不同于一维差分数组，二维差分数组中[x1,y1]之后的正方形区域都会+c。
//因此需要将[x1,y2+1]和[x2+1,y1]之后的区域-c,还要给[x2+1,y2+1]+c
void insert(int x1, int y1, int x2, int y2, int c) {
    s[x1][y1] += c;
    s[x1][y2 + 1] -= c;
    s[x2 + 1][y1] -= c;
    s[x2 + 1][y2 + 1] += c;
}

int main() {
    int n, m, q;
    scanf("%d%d%d", &n, &m, &q);
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= m; ++j) {
            scanf("%d", &a[i][j]);
            insert(i, j, i, j, a[i][j]);
        }
    }
    int x1, y1, x2, y2, c;
    while (q--) {
        scanf("%d%d%d%d%d", &x1, &y1, &x2, &y2, &c);
        insert(x1, y1, x2, y2, c);
    }
    //需要注意这里是在差分数组的基础上进行前缀和的计算，所以都是+=操作
    for (int i = 1; i <= n; ++i)
        for (int j = 1; j <= m; ++j)
            s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= m; ++j)
            printf("%d ", s[i][j]);
        printf("\n");
    }
    return 0;

799. 最长连续不重复子序列
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include <iostream>

using namespace std;
const int N = 1e6 + 10;
//数组q记录题目信息，数组s记录下标数字出现的次数
int q[N], s[N];

int main() {
    int n, res = 0;
    scanf("%d", &n);
    for (int i = 0; i < n; ++i) scanf("%d", &q[i]);
    //j在前，i在后
    //当s[q[i]]>1时说明有重复数字，此时，j向后移动至q[i]第一次出现的位置的后一个，此过程中将所有j经过的数字对应的s[q[j]]--
    for (int i = 0, j = 0; i < n; ++i) {
        ++s[q[i]];
        while (s[q[i]] > 1) --s[q[j++]];
        res = i - j + 1 > res ? i - j + 1 : res;
    }
    printf("%d", res);
    return 0;
}

801~900

801. 二进制中1的个数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include <iostream>

using namespace std;
int lowbit(int x){
    return x&-x;
}
int main() {
    int n;
    scanf("%d", &n);
    while (n--) {
        int res=0,x;
        scanf("%d",&x);
        while (x){
            x-=lowbit(x);
            ++res;
        }
        printf("%d ",res);
    }
    return 0;
}
802. 区间和
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;
const int N = 3 * 1e5 + 10;
typedef pair<int, int> PAIR;
//存放插入与查询信息
vector<PAIR> add, query;
//存放计算区间和的差分数组和前缀和数组
int a[N], s[N];
//alls存放对应索引信息
vector<int> alls;

//unique的自己实现
vector<int> unique(vector<int> &A){
	int j=0;
	for(int i=0;i<A.size();i++){
        //要么是第一个数要么不重复
		if(!i||A[i]!=A[i-1]) A[j++]=A[i];
	}
    return A.begin()+j;
}

int find(int x) {
    int l = 0, r = alls.size() - 1;
    while (l < r) {
        int mid = l + r >> 1;
        if (alls[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return l;
}

int main() {
    int n, m, index, data, l, r;
    scanf("%d%d", &n, &m);
    //step1 将所有用到的位置索引存入alls容器中,将相应的插入信息与查询信息存入add和query中
    for (int i = 0; i < n; ++i) {
        scanf("%d%d", &index, &data);
        add.push_back({index, data});
        alls.push_back(index);
    }
    for (int i = 0; i < m; ++i) {
        scanf("%d%d", &l, &r);
        query.push_back({l, r});
        alls.push_back(l);
        alls.push_back(r);
    }
    //step2 索引位置去重,此时alls下标就是相应索引映射后的位置
    sort(alls.begin(), alls.end());
    alls.erase(unique(alls.begin(), alls.end()), alls.end());
    //step3 插入数据
    for (auto item: add) a[find(item.first)] += item.second;
    //step4 计算前缀和
    for (int i = 1; i <= alls.size(); ++i) s[i] += s[i - 1] + a[i];
    //step5 返回结果
    for (auto item :query) {
        printf("%d\n", s[find(item.second)] - s[find(item.first) - 1]);
    }
    return 0;
}
803. 区间合并
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;
typedef pair<int, int> PAIR;
vector<PAIR> all;

vector<PAIR> merge(vector<PAIR> &x) {
    vector<PAIR> res;
    sort(x.begin(), x.end());
    int st = -2e9, ed = -2e9;
    for (auto itor:x) {
        if (ed < itor.first) {
            if (st != -2e9)res.push_back({st, ed});
            st = itor.first;
            ed = itor.second;
        } else {
            ed = max(ed, itor.second);
        }

    }
    //将最后一组加入结果集，需要判断st!=-2e9避免传入空数组
    if (st != -2e9) res.push_back({st, ed});
    return res;
}

int main() {
    int n, l, r;
    scanf("%d", &n);
    while (n--) {
        scanf("%d%d", &l, &r);
        all.push_back({l, r});
    }
    printf("%d", merge(all).size());
    return 0;
}
823.模拟栈
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <iostream>
#include <cstring>

using namespace std;
const int N = 1e6 + 10;
int stk[N], top = -1;

void push(int x) {
    stk[++top] = x;
}

int pop() {
    return stk[top--];
}

const char *empty() {
    return top == -1 ? "YES" : "NO";
}

int query() {
    return stk[top];
}

int main() {
    int n;
    char op[6];
    scanf("%d", &n);
    while (n--) {
        int x;
        scanf("%s", &op);
        if (!strcmp(op, "push")) {
            scanf("%d", &x);
            push(x);
        }
        if (!strcmp(op, "pop")) pop();
        if (!strcmp(op, "empty")) printf("%s\n", empty());
        if (!strcmp(op, "query")) printf("%d\n", query());
    }
    return 0;
}
826.单链表

本题注意当删除头节点时，需要特判。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include <iostream>

using namespace std;
const int N = 1e6 + 10;
int e[N], ne[N];
int idx = 0, head = -1;

void insertFromHead(int x) {
    e[idx] = x;
    ne[idx] = head;
    head = idx++;
}

void insert(int k, int x) {
    e[idx] = x;
    ne[idx] = ne[k];
    ne[k] = idx++;
}

void pop(int k) {
    ne[k] = ne[ne[k]];
}

int main() {
    int m;
    char method;
    scanf("%d", &m);
    while (m--) {
        getchar();
        scanf("%c", &method);
        if (method == 'H') {
            int x;
            scanf("%d", &x);
            insertFromHead(x);
        }
        if (method == 'D') {
            int k;
            scanf("%d", &k);
            if (!k) head = ne[head];
            else pop(k - 1);
        }
        if (method == 'I') {
            int k, x;
            scanf("%d%d", &k, &x);
            insert(k - 1, x);
        }
    }
    for (int i = head; i != -1; i = ne[i]) printf("%d ", e[i]);
    return 0;
}
827.双链表
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#include <iostream>
#include <cstring>

using namespace std;
const int N = 1e6 + 10;
int l[N], r[N], e[N];
int idx;

void init() {
    //0代表起始端点，1代表结束端点
    //真实数字从idx==2开始存放
    idx = 2;
    l[1] = 0;
    r[0] = 1;
}

//此函数的逻辑是插入k的右侧节点
//若需要实现插入k的左侧节点只需传入l[k]即可
void add(int k, int v) {
    e[idx] = v;
    l[idx] = k;
    r[idx] = r[k];
    l[r[k]] = idx;
    r[k] = idx;
    ++idx;
}

void remove(int k) {
    r[l[k]] = r[k];
    l[r[k]] = l[k];
}


int main() {
    int n;
    init();
    scanf("%d", &n);
    while (n--) {
        char op[3];
        int x, y;
        scanf("%s", &op);
        if (!strcmp("L", op)) {
            scanf("%d", &x);
            add(0, x);
        }
        if (!strcmp("R", op)) {
            scanf("%d", &x);
            add(l[1], x);
        }
        if (!strcmp("D", op)) {
            scanf("%d", &x);
            remove(x + 1);
        }
        if (!strcmp("IL", op)) {
            scanf("%d%d", &x, &y);
            add(l[x + 1], y);
        }
        if (!strcmp("IR", op)) {
            scanf("%d%d", &x, &y);
            add(x + 1, y);
        }
    }
    for (int i = r[0]; i != 1; i = r[i]) printf("%d ", e[i]);
    return 0;
}
829.模拟队列
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include <iostream>
#include <cstring>

using namespace std;
const int N = 1e6 + 10;
int e[N], head, tail;

void init() {
    head = 0;
    tail = -1;
}

void push(int x) {
    e[tail++] = x;
}

void pop() {
    ++head;
}

int query() {
    return e[head];
}

const char *empty() {
    return tail > head ? "NO" : "YES";
}

int main() {
    int n;
    scanf("%d", &n);
    char op[6];
    int x;
    while (n--) {
        scanf("%s", &op);
        if (!strcmp(op, "push")) {
            scanf("%d", &x);
            push(x);
        }
        if (!strcmp(op, "pop")) pop();
        if (!strcmp(op, "empty")) printf("%s\n", empty());
        if (!strcmp(op, "query")) printf("%d\n", query());
    }
    return 0;
}
830.单调栈

本题利用栈的性质

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include <iostream>

using namespace std;
const int N = 1e5 + 10;
int stk[N], top = -1;

int main() {
    int n, x;
    scanf("%d", &n);
    while (n--) {
        scanf("%d", &x);
        while (top != -1 && stk[top] >= x) --top;
        if (top != -1) printf("%d ", stk[top]);
        else printf("-1 ");
        //注意，需要将当前数字压入栈中
        stk[++top] = x;
    }
    return 0;
}
831.KMP字符串
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
.#include <iostream>
#include <cstring>
#include <vector>

using namespace std;
const int N = 1e5 + 10, M = 1e6 + 10;
char p[N], s[M];
vector<int> ne;

// brute force暴力枚举算法
// 复杂度为O(n*m)。当n和m为1e5数量级时，算法完全不可用。
void bruteForce(char *S, char *P) {
    int lens = strlen(S), lenp = strlen(P);
    for (int i = 0; i <= lens - lenp; ++i) {
        bool flag = true;
        for (int j = 0; P[j] != '\0'; ++j) {
            if (S[i + j] != P[j]) {
                flag = false;
                break;
            }
        }
        if (flag) printf("%d ", i);
    }
}

// KMP算法
// 复杂度为O(m+n)
void build(const char *pattern) {
    int len = strlen(pattern);
    ne.resize(len + 1);
    for (int i = 0, j = ne[0] = -1; i < len; ne[++i] = ++j) {
        while (~j && pattern[j] != pattern[i]) j = ne[j];
    }
}

vector<int> match(const char *text, const char *pattern) {
    vector<int> res;
    int lenp = strlen(pattern), lent = strlen(text);
    build(pattern);
    for (int i = 0, j = 0; i < lent; ++i) {
        while (j > 0 && text[i] != pattern[j]) j = ne[j];
        if (text[i] == pattern[j]) ++j;
        if (j == lenp) res.push_back(i - lenp + 1), j = ne[j];
    }
    return res;
}

int main() {
    int n, m;
    scanf("%d", &n);
    getchar();
    for (int i = 0; i < n; ++i) scanf("%c", &p[i]);
    scanf("%d", &m);
    getchar();
    for (int i = 0; i < m; ++i) scanf("%c", &s[i]);
    auto res = match(s, p);
    for (auto itor:res) printf("%d ", itor);
    return 0;
}
835.Trie字符串统计
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include <iostream>

using namespace std;
const int N = 1e5 + 1;
int s[N][26], cnt[N], idx;
char op, str[N];

void insert(const char *str) {
    int p = 0;
    for (int i = 0; str[i]; ++i) {
        int u = str[i] - 'a';
        if (!s[p][u]) s[p][u] = ++idx;
        p = s[p][u];
    }
    ++cnt[p];
}

int query(const char *str) {
    int p = 0;
    for (int i = 0; str[i]; ++i) {
        int u = str[i] - 'a';
        if (!s[p][u]) return 0;
        p = s[p][u];
    }
    return cnt[p];
}

int main() {
    int n;

    scanf("%d", &n);
    getchar();
    while (n--) {
        scanf("%c", &op);
        getchar();
        scanf("%s", &str);
        getchar();
        if (op == 'I') insert(str);
        if (op == 'Q') printf("%d\n",query(str));
    }
    return 0;
}
836.合并集合
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include<iostream>

using namespace std;
const int N = 1e5 + 10;
int s[N];

// 返回idx的根节点+路径压缩
int find(int idx) {
    if (idx != s[idx]) s[idx] = find(s[idx]);
    return s[idx];
}

int main() {
    int n, m, a, b;
    scanf("%d%d", &n, &m);
    char op[2];
    for (int i = 1; i <= n; i++) s[i] = i;
    while (m--) {
        scanf("%s%d%d", &op, &a, &b);
        if (op[0] == 'M') s[find(a)] = find(b);
        else {
            if (find(a) == find(b)) printf("Yes\n");
            else printf("No\n");
        }
    }
    return 0;
}
837.连通块中点的数量
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include<iostream>

using namespace std;
const int N = 1e5 + 10;
int s[N], sizeTable[N];

int find(int idx) {
    if (s[idx] != idx) s[idx] = find(s[idx]);
    return s[idx];
}

int main() {
    int n, m;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++) {
        s[i] = i;
        sizeTable[i] = 1;
    }
    char op[3];
    int a, b;
    while (m--) {
        scanf("%s", &op);
        if (op[0] == 'C') {
            scanf("%d%d", &a, &b);
            // 注意这里可能会同一个数内节点合并，这会导致sizeTable被多加节点，需要特判这种情况
            if (find(a) != find(b)) {
                sizeTable[find(b)] += sizeTable[find(a)];
                s[find(a)] = find(b);
            }
        } else {
            if (op[1] == '1') {
                scanf("%d%d", &a, &b);
                if (find(a) == find(b)) printf("Yes\n");
                else printf("No\n");
            } else {
                scanf("%d", &a);
                printf("%d\n", sizeTable[find(a)]);
            }
        }
    }
    return 0;
}
838.堆排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include <iostream>

using namespace std;
const int N = 1e5 + 10;
int s[N], len;

void down(int idx) {
    int min = idx;
    if (2 * idx <= len && s[2 * idx] < s[min]) min = 2 * idx;
    if (2 * idx + 1 <= len && s[2 * idx + 1] < s[min]) min = 2 * idx + 1;
    if (idx != min) {
        swap(s[idx], s[min]);
        down(min);
    }
}

int main() {
    int n, m;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++) scanf("%d", &s[i]);
    len = n;
    // 建堆
    for (int i = n >> 1; i; i--) down(i);
    while (m--) {
        printf("%d ", s[1]);
        s[1] = s[len--];
        down(1);
    }
    return 0;
}
839. 模拟堆
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
//
// Created by king on 2022/2/14.
//

#include <iostream>
#include <cstring>

using namespace std;
const int N = 1e5 + 10;
// h: 堆数据
// ph[i]: 第k数的堆索引
// hp[i]: 索引i是第hp[i]个插入的数
// len: 堆索引
int h[N], ph[N], hp[N], len;

// 这里的ab都是堆中的索引
void heapSwap(int a, int b) {
    swap(ph[hp[a]], ph[hp[b]]);
    swap(hp[a], hp[b]);
    swap(h[a], h[b]);
}

void down(int idx) {
    int t = idx;
    while (t && 2 * t <= len) {
        idx = t;
        if (2 * idx <= len && h[idx * 2] < h[t]) t = 2 * idx;
        if (2 * idx + 1 <= len && h[idx * 2 + 1] < h[t]) t = 2 * idx + 1;
        if (t != idx) heapSwap(idx, t);
        else break;
    }
}

void up(int idx) {
    while (idx >> 1 && h[idx >> 1] > h[idx]) {
        heapSwap(idx, idx / 2);
        idx /= 2;
    }
}

int main() {
    // n: 操作数量
    // x: 操作数
    // m: 第m个数
    int n, x, y, m = 0;
    scanf("%d", &n);
    char op[3];
    while (n--) {
        scanf("%s", op);
        if (!strcmp(op, "I")) {
            scanf("%d", &x);
            ph[++m] = ++len;
            hp[len] = m;
            h[len] = x;
            up(len);
        } else if (!strcmp(op, "PM"))
            printf("%d\n", h[1]);
        else if (!strcmp(op, "DM")) {
            heapSwap(1, len--);
            down(1);
        } else if (!strcmp(op, "D")) {
            scanf("%d", &x);
            int k = ph[x];
            heapSwap(k, len--);
            down(k);
            up(k);
        } else if (!strcmp(op, "C")) {
            scanf("%d%d", &x, &y);
            h[ph[x]] = y;
            down(ph[x]);
            up(ph[x]);
        }
    }
    return 0;
}

840. 模拟散列表

拉链法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include<iostream>
#include<cstring>

using namespace std;
const int N = 1e5 + 3;
int h[N], e[N], ne[N], idx;

void insert(int value) {
    int k = (value % N + N) % N;
    e[idx] = value;
    ne[idx] = h[k];
    h[k] = idx++;
}

bool find(int value) {
    int k = (value % N + N) % N;
    for (int i = h[k]; i != -1; i = ne[i]) {
        if (e[i] == value) return true;
    }
    return false;
}

int main() {
    memset(h, -1, sizeof h);
    int n, x;
    scanf("%d", &n);
    char op[2];
    while (n--) {
        scanf("%s%d", op, &x);
        if (op[0] == 'I') {
            insert(x);
        } else {
            if (find(x)) printf("Yes\n");
            else printf("No\n");
        }
    }
    return 0;
}

开放寻址法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include<iostream>
#include<cstring>

using namespace std;
const int N = 2e5 + 3;
const int Max = 0x3f3f3f3f;
// h是存放数据对应的key
int h[N];

// 如果x在哈希表中，返回x的下标；如果x不在哈希表中，返回x应该插入的位置
int find(int value) {
    // 保证获取的余数是整数，如果直接计算或者直接+N计算都会导致余数为负数
    int k = (value % N + N) % N;
    while (h[k] != Max && h[k] != value) {
        ++k;
        if (k == N) k = 0;
    }
    return k;
}

int main() {
    memset(h, 0x3f, sizeof h);
    int n, x;
    scanf("%d", &n);
    char op[2];
    while (n--) {
        scanf("%s%d", op, &x);
        if (op[0] == 'I') {
            h[find(x)] = x;
        } else {
            if (h[find(x)] != Max) printf("Yes\n");
            else printf("No\n");
        }
    }
    return 0;
}
841. 字符串哈希
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include <iostream>

using namespace std;
const int N = 1e5 + 3, P = 131;
// unsigned long long 天然维护了一个64位的2进制数组
typedef unsigned long long ULL;
// p数组表示的是p进制每一位对应的数
// h数组表示对应子串的ASCII码在p进制下对应的数值
// op存放字符串
int h[N], p[N];
char op[N];

ULL find(int l, int r) {
    return h[r] - h[l - 1] * p[r - l + 1];
}

int main() {
    int n, m;
    // 这里存op+1的位置存放字符串
    scanf("%d%d%s", &n, &m, op + 1);
    // 表示p进制的0次方
    p[0] = 1;
    for (int i = 1; i <= n; i++) {
        p[i] = p[i - 1] * P;
        h[i] = h[i - 1] * P + op[i];
    }
    int a, b, c, d;
    while (m--) {
        scanf("%d%d%d%d", &a, &b, &c, &d);
        if (find(a, b) == find(c, d)) printf("Yes\n");
        else printf("No\n");
    }
    return 0;
}
843. n-皇后问题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <iostream>

using namespace std;
int n;
const int N = 10;
bool col[N], dg[N], udg[N];
char g[N][N];

void dfs(int u) {
    if (u == n) {
        for (int i = 0; i < n; i++)puts(g[i]);
        puts("");
    } else {
        for (int i = 0; i < n; ++i) {
            // 查找列上没有皇后、正对角线和反对角线没有皇后
            // i表示列,u表述行
            if (!col[i] && !dg[u + i] && !udg[n - u + i]) {
                g[u][i] = 'Q';
                col[i] = dg[u + i] = udg[n - u + i] = true;
                dfs(u + 1);
                // 回复现场
                col[i] = dg[u + i] = udg[n - u + i] = false;
                g[u][i] = '.';
            }
        }
    }
}

int main() {
    scanf("%d", &n);
    // 初始化结果队列
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            g[i][j] = '.';
        }
    }
    dfs(0);
    return 0;
}
844.走迷宫
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;
typedef pair<int, int> PII;

const int N = 110;

int n, m;
// g存储图，d存储每个点到起点的距离
int g[N][N], d[N][N];
// q为bfs过程中的队列存储当前需要访问的节点，pre存储过来的路径
PII q[N * N], pre[N][N];

int bfs() {
    // 初始化d
    memset(d, -1, sizeof d);
    d[0][0] = 0;
    // 初始化队列，由于(0,0)必然放在队列中
    int hh, tt = 0;
    // 给予起点
    q[0] = {0, 0};
    // 上下左右的前进方式向量化表示
    int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
    while (hh <= tt) {
        auto t = q[hh++];
        int x, y;
        for (int i = 0; i < 4; ++i) {
            x = t.first + dx[i], y = t.second + dy[i];
            if (x >= 0 && x < n && y >= 0 && y < n && d[x][y] == -1 && !g[x][y]) {
                pre[x][y] = t;
                q[++tt] = {x, y};
                d[x][y] = d[t.first][t.second] + 1;
            }
        }
    }
    int x = n - 1, y = m - 1;
    while (x || y) {
        printf("(%d,%d) ", x, y);
        auto t = pre[x][y];
        x = t.first, y = t.second;
    }
    // 返回迷宫出口处的路径长度
    return d[n - 1][m - 1];
}

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < m; ++j) {
            scanf("%d", &g[i][j]);
        }
    }
    printf("%d", bfs());
    return 0;
}
846.树的重心
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <iostream>
#include <cstring>

using namespace std;
int n;
const int N = 100010, M = N * 2;
// h记录了图里面所有节点的尾指针
// idx表示e和ne中当前使用
int h[N], e[M], ne[M], idx;
// st记录每条边的情况
bool st[N];
int ans = N;

//链表头插法
void add(int a, int b) {
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}

// 以u为根的子树大小
int dfs(int u) {
    // 表示这条边已经被搜索过了
    st[u] = true;
    // sum：当前这个节点及其子树中所有节点的数量
    // res：当前这个节点之外所有子节点的数量
    int sum = 1, res = 0;
    // 遍历这个节点的所有连通节点
    for (int i = h[u]; i != -1; i = ne[i]) {
        int j = e[i];
        if (!st[j]) {
            int s = dfs(j);
            res = max(s, res);
            sum += s;
        }
    }
    res = max(n - sum, res);
    ans = min(ans, res);
    return sum;
}

int main() {
    memset(h, -1, sizeof h);
    scanf("%d", &n);
    int a, b;
    for (int i = 0; i < n - 1; ++i) {
        scanf("%d%d", &a, &b);
        add(a, b), add(b, a);
    }
    dfs(1);
    printf("%d", ans);
    return 0;
}
847.图中点的层次
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include <iostream>
#include <cstring>

using namespace std;
const int N = 1e5 + 10;
int n, m;
int e[N], ne[N], h[N], idx;
// d表示距离，q表示队列
int d[N], q[N];

void add(int a, int b) {
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}

int bfs() {
    memset(d, -1, sizeof d);
    d[1] = 0;
    int hh = 0, tt = 0;
    q[0] = 1;
    while (hh <= tt) {
        // t 当前队列中的x
        int t = q[hh++];
        // i 当前x的连通节点的idx
        for (int i = h[t]; i != -1; i = ne[i]) {
            int j = e[i];
            if (d[j] == -1) {
                d[j] = d[t] + 1;
                q[++tt] = j;
            }
        }
    }
    return d[n];
}

int main() {
    memset(h, -1, sizeof h);
    idx = 0;
    scanf("%d%d", &n, &m);
    int a, b;
    for (int i = 0; i < m; ++i) {
        scanf("%d%d", &a, &b);
        add(a, b);
    }

    printf("%d", bfs());
    return 0;
}
848.有向图的拓扑排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include <iostream>
#include <cstring>

using namespace std;
const int N = 1e6 + 10;
// 这里就是常见的邻接表表示方式，d表示入度
int e[N], ne[N], h[N], d[N], q[N], idx, n, m;

void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a];
    h[a] = idx++;
    d[b]++;
}

bool topsort() {
    int hh = 0, tt = -1;
    // 首先找出入度为0的点
    for (int i = 1; i <= n; ++i) {
        if (!d[i]) q[++tt] = i;
    }
    if (tt == -1) return false;
    while (hh <= tt) {
        // 找到其连通节点，去掉之前的入度检查是否为入度0节点
        int t = q[hh++];
        for (int i = h[t]; i != -1; i = ne[i]) {
            int j = e[i];
            d[j] -= 1;
            if (!d[j]) q[++tt] = j;
        }
    }
    return tt == n - 1;
}

int main() {
    memset(h, -1, sizeof h);
    scanf("%d%d", &n, &m);
    int a, b;
    for (int i = 0; i < m; ++i) {
        scanf("%d%d", &a, &b);
        add(a, b);
    }
    if (topsort()) {
        for (int i = 0; i < n; ++i) {
            printf("%d ", q[i]);
        }
    } else printf("-1");
    return 0;
}
849.Dijkstra求最短路
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <iostream>
#include <cstring>

using namespace std;
const int N = 510;
int n, m;
int g[N][N], dist[N];
bool st[N];

int dijkstra(int index) {
    memset(dist, 0x3f, sizeof dist);
    // 起点不能直接放在已遍过的集合中，因为需要起点更新dist，直接跳过起点，将无法更新之后的dist
    dist[index] = 0;
    for (int i = 1; i <= n; ++i) {
        // t为当前在集合中最近的点
        int t = -1; // 在还未确定最短路的点中，寻找距离最小的点
        for (int j = 1; j <= n; ++j)
            if (!st[j] && (t == -1 || dist[t] > dist[j]))t = j;
        if (t==n) break;
        st[t] = true;
        // 用t更新其他点的距离
        for (int j = 1; j <= n; ++j) dist[j] = min(dist[j], dist[t] + g[t][j]);
    }
    // 如果之后是0x3f3f3f3f则表明不是该点无法到达
    if (dist[n] == 0x3f3f3f3f) return -1;
    else return dist[n];
}

int main() {
    scanf("%d%d", &n, &m);
    memset(g, 0x3f, sizeof g);
    int a, b, c;
    while (m--) {
        scanf("%d%d%d", &a, &b, &c);
        g[a][b] = min(g[a][b], c);
    }
    printf("%d", dijkstra(1));
    return 0;
}
850.Dijkstra求最短路
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include <cstring>
#include <queue>

using namespace std;
int n, m;
const int N = 1e5 + 10;
int h[N], e[N], ne[N], w[N], dist[N], idx;
bool st[N];
typedef pair<int, int> PII;

int dijkstra(int index) {
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    // 创建小根堆
    priority_queue<PII, vector<PII>, greater<PII>> heap;
    heap.push({0, 1});
    while (heap.size()) {
        auto t = heap.top();
        heap.pop();
        int ver = t.second, distance = t.first;
        // 跳过冗余节点
        if (st[ver]) continue;
        st[ver] = true;
        for (int i = h[ver]; i != -1; i = ne[i]) {
            int j = e[i];
            if (dist[j] > distance + w[i]) {
                dist[j] = distance + w[i];
                heap.push({dist[j], j});
            }
        }
    }
    if (dist[n] == 0x3f3f3f3f) return -1;
    else return dist[n];
}

void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

int main() {
    scanf("%d%d", &n, &m);
    // 尚未初始化时，节点都没有链接节点
    memset(h, -1, sizeof h);
    int a, b, c;
    while (m--) {
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c);
    }
    printf("%d", dijkstra(1));
    return 0;
}
851~900
[851.spfa求最短路]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include <cstring>
#include <queue>

using namespace std;
int n, m;
const int N = 1e5 + 10;
int h[N], e[N], ne[N], w[N], dist[N], idx;
bool st[N];
typedef pair<int, int> PII;

int spfa(int index) {
    memset(dist, 0x3f, sizeof dist);
    dist[index] = 0;
    queue<int> q;
    st[index] = true;
    q.push(index);
    while (q.size()) {
        auto t = q.front();
        q.pop();
        st[t] = false;
        for (int i = h[t]; i != -1; i = ne[i]) {
            auto it = e[i];
            if (dist[it] > dist[t] + w[i]) {
                dist[it] = dist[t] + w[i];
                if (!st[it]) {
                    st[it] = true;
                    q.push(it);
                }
            }
        }
    }
    return dist[n];
}

void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

int main() {
    scanf("%d%d", &n, &m);
    // 尚未初始化时，节点都没有链接节点
    memset(h, -1, sizeof h);
    int a, b, c;
    while (m--) {
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c);
    }
    int result = spfa(1);
    if (result > 0x3f3f3f3f / 2) puts("impossible");
    else printf("%d", result);
    return 0;
}
[852.spfa判断负环]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#include <cstring>
#include <queue>
#include <cstdio>
using namespace std;
int n, m;
const int N = 1e5 + 10;
int h[N], e[N], ne[N], w[N], idx;
bool st[N];
// dist[x]存储1号点到x的最短距离，cnt[x]存储1到x的最短路中经过的点数
int cnt[N], dist[N];

void add(int a, int b, int x) {
    e[idx] = b;
    w[idx] = x;
    ne[idx] = h[a];
    h[a] = idx++;
}

bool spfa() {
    queue<int> q;
    // 避免出现起点通路上没有负环，因此直接加入所有点
    for (int i = 1; i <= n; ++i) {
        q.push(i);
        st[i] = true;
    }
    while (q.size()) {
        int t = q.front();
        q.pop();
        st[t] = false;
        for (int i = h[t]; i != -1; i = ne[i]) {
            int j = e[i];
            if (dist[j] > dist[t] + w[i]) {
                dist[j] = dist[t] + w[i];
                cnt[j] = cnt[t] + 1;
                if (cnt[j] > n) return true;
                if (!st[j]) {
                    st[j] = true;
                    q.push(j);
                }
            }
        }
    }
    return false;
}

int main() {
    memset(h, -1, sizeof h);
    scanf("%d%d", &n, &m);
    int a, b, x;
    for (int i = 0; i < m; ++i) {
        scanf("%d%d%d", &a, &b, &x);
        add(a, b, x);
    }
    if (spfa()) puts("Yes");
    else puts("No");
}
[853.有边数限制的最短路]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include <iostream>
#include <cstring>
#include <algorithm>

const int N = 510, M = 10010;
int n, m, k;
int dist[N], backup[N];
struct Edge {
    int a, b, w;
} edges[M];

int bellman_ford() {
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    // 这里的k限制了最多能走的边数
    for (int i = 0; i < k; ++i) {
        // 需要注意这里一定要备份之前的数组，不然会出现更新m条边时使用了本次循环更新的dist
        memcpy(backup, dist, sizeof dist);
        for (int j = 0; j < m; ++j) {
            int a = edges[j].a, b = edges[j].b, w = edges[j].w;
            dist[b] = std::min(dist[b], backup[a] + w);
        }
    }
    return dist[n];
}

int main() {
    scanf("%d%d%d", &n, &m, &k);
    int a, b, x;
    for (int i = 0; i < m; ++i) {
        scanf("%d%d%d", &edges[i].a, &edges[i].b, &edges[i].w);
    }
    int t = bellman_ford();
    if (t > 0x3f3f3f3f / 2)puts("impossible");
    else printf("%d\n", t);
    return 0;
}
[854.Floyd求最短路]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include <cstdio>
#include <algorithm>

const int N = 210, INF = 1e9;
int n, m, k;
int dist[N][N];

void floyd() {
    for (int k = 1; k <= n; ++k) {
        for (int i = 1; i <= n; ++i) {
            for (int j = 1; j <= n; ++j) {
                dist[i][j] = std::min(dist[i][j], dist[i][k] + dist[k][j]);
            }
        }
    }
}

int main() {
    scanf("%d%d%d", &n, &m, &k);
    int a, b, w;
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= n; ++j) {
            dist[i][j] = i == j ? 0 : INF;
        }
    }
    for (int i = 0; i < m; ++i) {
        scanf("%d%d%d", &a, &b, &w);
        dist[a][b] = std::min(w, dist[a][b]);
    }
    floyd();
    for (int i = 0; i < k; ++i) {
        scanf("%d%d", &a, &b);
        if (dist[a][b] > INF >> 1) printf("impossible\n");
        else printf("%d\n", dist[a][b]);
    }
    return 0;
}
[858.Prim算法求最小生成树]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include <cstring>
#include <algorithm>
#include <cstdio>

const int N = 510;
int g[N][N], dist[N];
int n, m;
bool st[N];

int prim() {
    memset(dist, 0x3f, sizeof dist);
    // 记录最小生成树的路径之和
    int res = 0;
    for (int i = 0; i < n; ++i) {
        int t = -1;
        for (int j = 1; j <= n; ++j) {
            // 需要注意这里st比较的是j不是t
            if (!st[j] && (t == -1 || dist[j] < dist[t]))
                t = j;
        }
        // i=0时 dist刚初始化所有边都是INF
        if (i && dist[t] == 0x3f3f3f3f) return 0x3f3f3f3f;
        if (i) res += dist[t];
        st[t] = true;
        for (int j = 1; j <= n; ++j)dist[j] = std::min(dist[j], g[t][j]);
    }
    return res;
}

int main() {
    scanf("%d%d", &n, &m);
    int a, b, w;
    memset(g, 0x3f, sizeof g);
    for (int i = 0; i < m; ++i) {
        scanf("%d%d%d", &a, &b, &w);
        g[a][b] = g[b][a] = std::min(g[a][b], w);
    }
    int r = prim();
    if (r == 0x3f3f3f3f) puts("impossible");
    else printf("%d", r);
}
[859.Kruskal算法求最小生成树]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <cstdio>
#include <cstring>
#include <algorithm>

const int N = 200010;
int n, m;
int p[N];

struct Edge {
    int a, b, w;

    const bool operator<(const Edge &edge) const {
        return w < edge.w;
    }
} edges[N];

int find(int x) {
    if (p[x] != x) {
        p[x] = find(p[x]);
    }
    return p[x];
}

int kruskal() {
    int res = 0, cnt = 0;
    for (int i = 1; i <= n; ++i) p[i] = i;
    std::sort(edges, edges + m);
    int a, b, w;
    for (int i = 0; i < m; ++i) {
        a = edges[i].a, b = edges[i].b, w = edges[i].w;
        a = find(a), b = find(b);
        if (a != b) {
            res += w;
            cnt++;
            p[a] = b;
        }
    }
    if (cnt < n - 1) return 0x3f3f3f3f;
    else return res;
}

int main() {
    int a, b, c;
    scanf("%d%d", &n, &m);
    for (int i = 0; i < m; ++i) {
        scanf("%d%d%d", &a, &b, &c);
        edges[i] = {a, b, c};
    }
    int r = kruskal();
    if (r == 0x3f3f3f3f) puts("impossible");
    else printf("%d", r);
    return 0;
}
[860.染色法判断二分图]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#include <cstdio>
#include <cstring>
#include <algorithm>

const int N = 100010, M = 200010;
int n, m;
int h[N], e[M], ne[M], idx;
int color[N];

void add(int a, int b) {
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}

bool dfs(int index, int c) {
    color[index] = c;
    for (int i = h[index]; i != -1; i = ne[i]) {
        int j = e[i];
        if (!~color[j]) {
            if (!dfs(j, !c)) return false;
        } else {
            if (color[j] == c) return false;
        }
    }
    return true;
}

bool check() {
    bool flag = true;
    memset(color, -1, sizeof color);
    for (int i = 1; i <= n; ++i) {
        if (!~color[i]) {
            if (!dfs(i, 0)) {
                flag = false;
                break;
            }
        }
    }
    return flag;
}

int main() {
    scanf("%d%d", &n, &m);
    memset(h, -1, sizeof h);
    int a, b;
    for (int i = 0; i < m; ++i) {
        scanf("%d%d", &a, &b);
        if (a != b) {
            add(a, b), add(b, a);
        }
    }
    if (check()) puts("Yes");
    else puts("No");
    return 0;
}
[861.二分图的最大匹配]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include <cstdio>
#include <cstring>

int n1, n2, m;
const int N = 510, M = 5e5 + 10;
bool st[N];
int e[M], ne[M], idx, h[N];
int pair[N];

bool find(int index) {
    for (int i = h[index]; i != -1; i = ne[i]) {
        int j = e[i];
        if (!st[j]) {
            st[j] = true;
            // 当前没有匹配或者可以更换别的匹配
            if (pair[j] == -1 || find(pair[j])) {
                pair[j] = index;
                return true;
            }
        }
    }
    return false;
}

void match() {
    int res = 0;
    for (int i = 1; i <= n1; ++i) {
        // 需要每次清空之前的占位
        memset(st, false, sizeof st);
        if (find(i)) res += 1;
    }
    printf("%d", res);
}

void add(int x, int y) {
    e[idx] = y;
    ne[idx] = h[x];
    h[x] = idx++;
}

int main() {
    memset(h, -1, sizeof h);
    scanf("%d%d%d", &n1, &n2, &m);
    int x, y;
    for (int i = 0; i < m; ++i) {
        scanf("%d%d", &x, &y);
        add(x, y);
    }
    memset(pair, -1, sizeof pair);
    match();
    return 0;
}
[866.试除法判定质数]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include <cstdio>

bool is_prime(int x) {
    if (x < 2)return false;
    for (int i = 2; i <= x / i; ++i) {
        if (x % i == 0) return false;
    }
    return true;
}

int main() {
    int n,x;
    scanf("%d", &n);
    for(int i=0;i<n;++i){
        scanf("%d",&x);
        if (is_prime(x)) {
            puts("Yes");
        } else {
            puts("No");
        }
    }
    return 0;
}
[867.分解质因数]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include <cstdio>

void divide(int x) {
    for (int i = 2; i <= x / i; ++i) {
        if (x % i == 0) {
            int b = 0;
            while (x % i == 0) {
                x /= i;
                b += 1;
            }
            printf("%d %d\n", i, b);
        }
    }
    if (x > 1) printf("%d 1\n", x);
    puts("");
}

int main() {
    int n, x;
    scanf("%d", &n);
    for (int i = 0; i < n; ++i) {
        scanf("%d", &x);
        divide(x);
    }
    return 0;
}
[868.线性法筛质数]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <cstdio>

const int N = 1e6 + 10;
// primes[]存储所有素数
int primes[N], cnt;
// st[x]存储x是否被筛掉
bool st[N];

// 埃式筛法
void get_primes(int x) {
    for (int i = 2; i <= x; ++i) {
        if (!st[i]) {
            primes[cnt++] = i;
            for (int j = i + i; j <= x; j += i) st[j] = true;
        }
    }
}

// 线性筛法
void get_grimes_linear(int x) {
    for(int i=2;i<=x;++i){
        if(!st[i]) primes[cnt++]=i;
        for(int j=0;primes[j]*i<x;++j){
            st[i*primes[j]]= true;
            if(i% primes[j]==0) break;
        }
    }
}

int main() {
    int n;
    scanf("%d", &n);
    get_grimes_linear(n);
    printf("%d", cnt);
    return 0;
}
[869. 试除法求约数]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include <cstdio>
#include <vector>

std::vector<int> get_divisors(int x) {
    std::vector<int> result;
    for (int i = 1; i <= x / i; ++i) {
        if (x % i == 0) {
            result.push_back(i);
        }
    }
    int cnt = result.size();
    for (int i = cnt - 1; i >= 0; --i) if (x / result[i] != result[i]) result.push_back(x / result[i]);
    return result;
}

int main() {
    int n, x;
    scanf("%d", &n);
    for (int i = 0; i < n; ++i) {
        scanf("%d", &x);
        std::vector<int> result = get_divisors(x);
        for (auto &it: result) {
            printf("%d ", it);
        }
        puts("");
    }
}
[870.约数个数]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include <cstdio>
#include <unordered_map>

typedef long long LL;
const int mod = 1e9 + 7;

void get_divisor(std::unordered_map<int, int> &map, int x) {
    for (int i = 2; i <= x / i; ++i) {
        while (x % i == 0) {
            x /= i;
            map[i] += 1;
        }
    }
    if (x > 1) map[x] += 1;
}

int main() {
    int n, x;
    scanf("%d", &n);
    LL res = 1;
    std::unordered_map<int, int> divisors;
    for (int i = 0; i < n; ++i) {
        scanf("%d", &x);
        get_divisor(divisors, x);
    }
    for (auto &it: divisors) {
        res = (it.second + 1) * res % mod;
    }
    printf("%lld", res);
    return 0;
}
[871.约数之和]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include <cstdio>
#include <unordered_map>

const int mod = 1e9 + 7;
typedef long long LL;

void get_divisor(std::unordered_map<int, int> &map, int x) {
    for (int i = 2; i <= x / i; ++i) {
        while (x % i == 0) {
            x /= i;
            map[i] += 1;
        }
    }
    if (x > 1) map[x] += 1;
}

int main() {
    int n, x;
    scanf("%d", &n);
    std::unordered_map<int, int> map;
    LL res = 1;
    for (int i = 0; i < n; ++i) {
        scanf("%d", &x);
        get_divisor(map, x);
    }
    for (auto &it: map) {
        int p = it.first, a = it.second;
        LL t = 1;
        while (a--) t = (p * t + 1) % mod;
        res = res * t % mod;
    }
    printf("%lld", res);
    return 0;
}
[872.最大公约数]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include <iostream>

int gcd(int a, int b) {
    return b ? gcd(b, a % b) : a;
}

int main() {
    int n;
    scanf("%d", &n);
    int a, b;
    for (int i = 0; i < n; ++i) {
        scanf("%d%d", &a, &b);
        printf("%d\n", gcd(a, b));
    }
    return 0;
}
[873.欧拉函数]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include <cstdio>

int main() {
    int n, x;
    scanf("%d", &n);
    for (int i = 0; i < n; ++i) {
        scanf("%d", &x);
        int res = x;
        for (int i = 2; i <= x / i; ++i) {
            if (x % i == 0) {
                res = res / i * (i - 1);
                while (x % i == 0) x /= i;
            }
        }
        if (x > 1) res = res / x * (x - 1);
        printf("%d\n", res);
    }
    return 0;
}

901~1000

1001～2000

1001～1500

1001～1100

1076,迷宫问题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include <iostream>
#include <cstring>

using namespace std;
const int N = 1010, M = N * N;
int n;
typedef pair<int, int> PII;
// 注意这的大小  q数组会保存最多所有点的移动信息，需要开辟较大空间
PII q[M], pre[N][N];
int d[N][N], g[N][N];

void bfs() {
    int hh = 0, tt = 0;
    memset(d, -1, sizeof(d));
    d[n - 1][n - 1] = 0;
    q[0] = {n - 1, n - 1};
    const int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, -1, 0, 1};
    while (hh <= tt) {
        auto t = q[hh++];
        for (int i = 0; i < 4; ++i) {
            int x = t.first + dx[i], y = t.second + dy[i];
            if (x >= 0 && x < n && y >= 0 && y < n && d[x][y] == -1 && g[x][y] == 0) {
                pre[x][y] = t;
                q[++tt] = {x, y};
                d[x][y] = d[t.first][t.second] + 1;
            }
        }
    }
    int x = 0, y = 0;
    while (true) {
        printf("%d %d\n", x, y);
        auto it = pre[x][y];
        if (x == n - 1 && y == n - 1) break;
        x = it.first, y = it.second;
    }
}

int main() {
    scanf("%d", &n);
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < n; ++j) {
            scanf("%d", &g[i][j]);
        }
    }
    bfs();
    return 0;
}

1101～1200

1201～1300

1301～1400

1381. 阶乘

本题重点在于如何获取最后一个非零的数。通过分解质因数可知，这里计算出来的阶乘可以拆分为 ,阶乘中的0就来源于这里的2和5之积，也就是k的数量。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <iostream>
using namespace std;
int main(){
    int n;
    scanf("%d",&n);
    //这里的d2表示因数中2的个数，d5表示5的个数
    int res=1,d2=0,d5=0;
    for(int i=1;i<=n;i++){
        int x=i;
        while(x%2==0) x/=2,d2+=1;
        while(x%5==0) x/=5,d5+=1;
        //这里取余可以有效的减小数字的大小，对于结果没有影响
        res=res*x%10;
    }
    //将多扣除的2或者5乘回去
    int k=d2<d5?d2:d5;
    //这里取余可以有效的减小数字的大小，对于结果没有影响
    for(int i=0;i<d2-k;i++) res=res*2%10;
    for(int i=0;i<d5-k;i++) res=res*5%10;
    printf("%d",res%10);
    return 0;
}

2001～3000

3001～4000

3001～3500

3001～3100

3100～3200

3192. 出现次数最多的数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include <iostream>

using namespace std;
const int N = 10000 + 10;
int q[N];

int main() {
    int n, num, min = 0;
    scanf("%d", &n);
    while (n--) {
        scanf("%d", &num);
        q[num] += 1;
    }
    for (int i = 0; i < N; i++) {
        if (q[min] < q[i]) min = i;
    }
    printf("%d", min);
    return 0;
}
文章作者: 不二
文章链接: http://buerlog.top/2021/03/23/suan-fa/acwing-shua-ti-ji-lu/
版权声明: 本博客所有文章除特別声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 不二 !
Cpp
赏
  目录